Beta Cell Turnover in Pancreatic Islet
How is the right islet size established during zebrafish pancreas development?
Introduction
Beta cells in the developing pancreas of zebrafish divide rapidly between 5 and 30 days post fertilization (dpf) and additional beta cells are recruited to the islet. Yet their overall number by 30 dpf remains well under control with the help of cell death.
Model Description
This Morpheus model combines four models of beta cell turnover in the pancreatic islet. One pair of models are ordinary differential equations for (the continuum approximation of) the beta cell number, the other pair are two-dimensional agent-based models (in z-layers ‘0’ for wildtype and ‘2’ for the mutant, separated by a fixed layer ‘1’) that explore stochastic effects of the combined cell behaviors and visualize the spatial density of cell death events. Of each pair, one model corresponds to the wildtype with all processes active and the other to the mutant.
Results
The following movie shows the agent-based simulation:
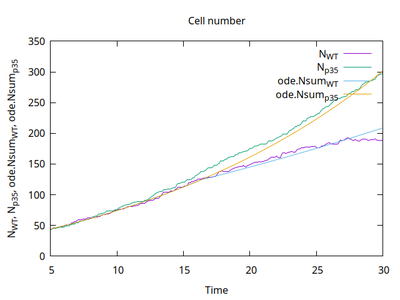
Cell numbers from the simulation above are shown in the following graph and compared to ODE simulations with the same rate constants:
Reference
This model is the original used in the publication, up to technical updates:
M. N. Akhtar, A. Hnatiuk, L. Delgadillo-Silva, S. Geravandi, K. Sameith, S. Reinhardt, K. Bernhardt, S. P. Singh, K. Maedler, L. Brusch, N. Ninov: Developmental beta-cell death orchestrates the islet’s inflammatory milieu by regulating immune system crosstalk. The EMBO Journal, 2025.
Model
M2986-pancreas-islet_model.xml
XML Preview
<?xml version='1.0' encoding='UTF-8'?>
<MorpheusModel version="4">
<Description>
<Title>M2986: Pancreas Turnover</Title>
<Details>Model ID: https://identifiers.org/morpheus/M2986
Full title: Beta Cell Turnover in Pancreatic Islet
Date: 20.09.2024
Authors: M. Akhtar et al.
Submitters: L. Brusch
Curators: D. Jahn
Software: Morpheus (open source). Download from: https://morpheus.gitlab.io
Units: [time] = 1 d
[space] = 1 µm
Reference: This Morpheus model was developed and analyzed in the original publication:
M. Akhtar et al.
</Details>
</Description>
<Space>
<Lattice class="cubic">
<Neighborhood>
<Order>optimal</Order>
</Neighborhood>
<Size symbol="size" value="200, 200, 3"/>
<BoundaryConditions>
<Condition type="noflux" boundary="x"/>
<Condition type="noflux" boundary="-x"/>
<Condition type="noflux" boundary="y"/>
<Condition type="noflux" boundary="-y"/>
<Condition type="noflux" boundary="z"/>
<Condition type="noflux" boundary="-z"/>
</BoundaryConditions>
</Lattice>
<SpaceSymbol symbol="space"/>
</Space>
<Time>
<StartTime value="0"/>
<StopTime value="30"/>
<TimeSymbol symbol="time" name="Time (dpf)"/>
</Time>
<Analysis>
<ModelGraph format="dot" reduced="false" include-tags="#untagged"/>
<Gnuplotter time-step="0.1">
<Terminal name="png"/>
<Plot title="WT cells" slice="0">
<Cells max="5" min="0" value="cell.type">
<ColorMap adaptive-range="false">
<Color value="0" color="white"/>
<Color value="1" color="green"/>
<Color value="2" color="red"/>
<Color value="3" color="green"/>
<Color value="4" color="red"/>
<Color value="5" color="blue"/>
</ColorMap>
</Cells>
</Plot>
<Plot title="p35 cells" slice="2">
<Cells max="5" min="0" value="cell.type">
<ColorMap adaptive-range="false">
<Color value="0" color="white"/>
<Color value="1" color="green"/>
<Color value="2" color="red"/>
<Color value="3" color="green"/>
<Color value="4" color="red"/>
<Color value="5" color="blue"/>
</ColorMap>
</Cells>
</Plot>
</Gnuplotter>
<Logger time-step="0.1" name="Time courses">
<Input/>
<Output>
<TextOutput separator="comma" file-format="csv"/>
</Output>
<Plots>
<Plot time-step="-1" title="Cell number">
<Style style="lines"/>
<Terminal terminal="png"/>
<X-axis>
<Symbol symbol-ref="time"/>
</X-axis>
<Y-axis minimum="0" maximum="350">
<Symbol symbol-ref="N_WT"/>
<Symbol symbol-ref="N_p35"/>
<Symbol symbol-ref="ode.Nsum_WT"/>
<Symbol symbol-ref="ode.Nsum_p35"/>
</Y-axis>
</Plot>
</Plots>
<Restriction condition="time>time.start-0.1"/>
</Logger>
</Analysis>
<CellTypes>
<CellType class="medium" name="Medium"/>
<CellType class="biological" name="Cell_WT_p">
<VolumeConstraint target="V_target" strength="Lam_V"/>
<SurfaceConstraint target="1" strength="Lam_S" mode="aspherity"/>
<CellDivision division-plane="random">
<Condition>time >= time.birth+Tc</Condition>
<Triggers>
<Rule symbol-ref="Tc">
<Expression>exp(rand_norm(Tc.ln_mean,Tc.ln_std))</Expression>
</Rule>
<Rule symbol-ref="time.birth">
<Expression>time</Expression>
</Rule>
</Triggers>
</CellDivision>
<Property symbol="Tc" value="Tc.mean"/>
<Property symbol="time.birth" value="rand_uni(time.start-Tc,time.start)"/>
<Property symbol="time.inact" value="time.start"/>
<!-- <Disabled>
<CellDeath name="apoptosis">
<Condition>(time>=time.onset) and (time<time.onset+time.duration) and rand_uni(0,1)<(d*mcs_duration)</Condition>
</CellDeath>
</Disabled>
-->
<ChangeCellType time-step="mcs_duration" newCellType="Cell_WT_q" name="inactivation">
<Condition>rand_uni(0,1)<(k.inact*mcs_duration) and time>time.start</Condition>
<Triggers>
<Rule symbol-ref="time.inact">
<Expression>time</Expression>
</Rule>
</Triggers>
</ChangeCellType>
<AddCell name="neogenesis" overwrite="true">
<Count>(rand_uni(0,1)<(v*celltype.Cell_WT_p.size/N_WT*mcs_duration)) and (time>time.start)</Count>
<Distribution>space.z==0 and ((space.x-size.x/2)^2+(space.y-size.y/2)^2)<20^2</Distribution>
<Triggers>
<Rule symbol-ref="time.birth">
<Expression>time</Expression>
</Rule>
</Triggers>
</AddCell>
<ChangeCellType time-step="mcs_duration" newCellType="Cell_WT_apoptosis" name="apoptosis">
<Condition>(time>=time.onset) and (time<time.onset+time.duration) and rand_uni(0,1)<(d*mcs_duration)</Condition>
<Triggers>
<Rule symbol-ref="time.birth">
<Expression>time</Expression>
</Rule>
</Triggers>
</ChangeCellType>
</CellType>
<CellType class="biological" name="Cell_WT_q">
<VolumeConstraint target="V_target" strength="Lam_V"/>
<SurfaceConstraint target="1" strength="Lam_S" mode="aspherity"/>
<Property symbol="Tc" value="Tc.mean"/>
<Property symbol="time.birth" value="rand_uni(time.start-Tc,time.start)"/>
<Property symbol="time.inact" value="time.start"/>
<!-- <Disabled>
<CellDeath name="apoptosis">
<Condition>(time>=time.onset) and (time<time.onset+time.duration) and rand_uni(0,1)<(d*mcs_duration)</Condition>
</CellDeath>
</Disabled>
-->
<ChangeCellType time-step="mcs_duration" newCellType="Cell_WT_p" name="activation">
<Condition>rand_uni(0,1)<(k.act*mcs_duration) and time>time.start</Condition>
<Triggers>
<Rule symbol-ref="time.birth">
<Expression>time-(time.inact-time.birth)</Expression>
</Rule>
</Triggers>
</ChangeCellType>
<AddCell name="neogenesis" overwrite="true">
<Count>(rand_uni(0,1)<(v*celltype.Cell_WT_q.size/N_WT*mcs_duration)) and (time>time.start)</Count>
<Distribution>space.z==0 and ((space.x-size.x/2)^2+(space.y-size.y/2)^2)<20^2</Distribution>
<Triggers>
<Rule symbol-ref="time.birth">
<Expression>time</Expression>
</Rule>
</Triggers>
</AddCell>
<ChangeCellType time-step="mcs_duration" newCellType="Cell_WT_apoptosis" name="apoptosis">
<Condition>(time>=time.onset) and (time<time.onset+time.duration) and rand_uni(0,1)<(d*mcs_duration)</Condition>
<Triggers>
<Rule symbol-ref="time.birth">
<Expression>time</Expression>
</Rule>
</Triggers>
</ChangeCellType>
</CellType>
<CellType class="biological" name="Cell_p35_p">
<VolumeConstraint target="V_target" strength="Lam_V"/>
<SurfaceConstraint target="1" strength="Lam_S" mode="aspherity"/>
<CellDivision division-plane="random">
<Condition>time >= time.birth+Tc</Condition>
<Triggers>
<Rule symbol-ref="Tc">
<Expression>exp(rand_norm(Tc.ln_mean,Tc.ln_std))</Expression>
</Rule>
<Rule symbol-ref="time.birth">
<Expression>time</Expression>
</Rule>
</Triggers>
</CellDivision>
<Property symbol="Tc" value="Tc.mean"/>
<Property symbol="time.birth" value="rand_uni(time.start-Tc,time.start)"/>
<Property symbol="time.inact" value="time.start"/>
<ChangeCellType time-step="mcs_duration" newCellType="Cell_p35_q" name="inactivation">
<Condition>rand_uni(0,1)<(k.inact*mcs_duration) and time>time.start</Condition>
<Triggers>
<Rule symbol-ref="time.inact">
<Expression>time</Expression>
</Rule>
</Triggers>
</ChangeCellType>
<AddCell name="neogenesis" overwrite="true">
<Count>(rand_uni(0,1)<(v*celltype.Cell_p35_p.size/N_p35*mcs_duration)) and (time>time.start)</Count>
<Distribution>space.z==2 and ((space.x-size.x/2)^2+(space.y-size.y/2)^2)<20^2</Distribution>
<Triggers>
<Rule symbol-ref="time.birth">
<Expression>time</Expression>
</Rule>
</Triggers>
</AddCell>
</CellType>
<CellType class="biological" name="Cell_p35_q">
<VolumeConstraint target="V_target" strength="Lam_V"/>
<SurfaceConstraint target="1" strength="Lam_S" mode="aspherity"/>
<Property symbol="Tc" value="Tc.mean"/>
<Property symbol="time.birth" value="rand_uni(time.start-Tc,time.start)"/>
<Property symbol="time.inact" value="time.start"/>
<ChangeCellType time-step="mcs_duration" newCellType="Cell_p35_p" name="activation">
<Condition>rand_uni(0,1)<(k.act*mcs_duration) and time>time.start</Condition>
<Triggers>
<Rule symbol-ref="time.birth">
<Expression>time-(time.inact-time.birth)</Expression>
</Rule>
</Triggers>
</ChangeCellType>
<AddCell name="neogenesis" overwrite="true">
<Count>(rand_uni(0,1)<(v*celltype.Cell_p35_q.size/N_p35*mcs_duration)) and (time>time.start)</Count>
<Distribution>space.z==2 and ((space.x-size.x/2)^2+(space.y-size.y/2)^2)<20^2</Distribution>
<Triggers>
<Rule symbol-ref="time.birth">
<Expression>time</Expression>
</Rule>
</Triggers>
</AddCell>
</CellType>
<CellType class="biological" name="Separator">
<FreezeMotion>
<Condition>1</Condition>
</FreezeMotion>
</CellType>
<CellType class="biological" name="Cell_WT_apoptosis">
<VolumeConstraint target="V_target" strength="Lam_V"/>
<SurfaceConstraint target="1" strength="Lam_S" mode="aspherity"/>
<Property symbol="time.birth" value="0"/>
<CellDeath name="apoptosis">
<Condition>time>=time.birth+time.apoptotic</Condition>
</CellDeath>
</CellType>
</CellTypes>
<CPM>
<Interaction/>
<ShapeSurface scaling="norm">
<Neighborhood>
<Order>optimal</Order>
</Neighborhood>
</ShapeSurface>
<MonteCarloSampler stepper="edgelist">
<MCSDuration value="0.01"/>
<MetropolisKinetics temperature="1"/>
<Neighborhood>
<Order>optimal</Order>
</Neighborhood>
</MonteCarloSampler>
</CPM>
<CellPopulations>
<Population type="Separator" name="Separator" size="1">
<InitCellObjects mode="distance">
<Arrangement displacements="1, 1, 1" repetitions="1, 1, 1">
<Box origin="0.0, 0.0, 1.0" size="size.x, size.y, 1.0"/>
</Arrangement>
</InitCellObjects>
</Population>
<Population type="Cell_WT_p" name="3 proliferative WT" size="0">
<InitCircle number-of-cells="3" mode="regular">
<Dimensions radius="20.0" center="size.x/2, size.y/2, 0.0"/>
</InitCircle>
</Population>
<Population type="Cell_WT_q" name="41 quiescent WT" size="0">
<InitCircle number-of-cells="41" mode="regular">
<Dimensions radius="20.0" center="size.x/2, size.y/2, 0.0"/>
</InitCircle>
</Population>
<Population type="Cell_p35_p" name="3 proliferative p35" size="0">
<InitCircle number-of-cells="3" mode="regular">
<Dimensions radius="20.0" center="size.x/2, size.y/2, 2.0"/>
</InitCircle>
</Population>
<Population type="Cell_p35_q" name="41 quiescent p35" size="0">
<InitCircle number-of-cells="41" mode="regular">
<Dimensions radius="20.0" center="size.x/2, size.y/2, 2.0"/>
</InitCircle>
</Population>
</CellPopulations>
<Global>
<Constant symbol="V_target" value="100"/>
<Constant symbol="Lam_V" name="Volume strength" value="1"/>
<Constant symbol="Lam_S" name="Surface strangth" value="1"/>
<Constant symbol="Tc.mean" name="Mean cell cycle duration" value="1.05"/>
<Constant symbol="Tc.std" value="0.05"/>
<Constant symbol="Tc.ln_mean" value="ln(Tc.mean^2/sqrt(Tc.mean^2+Tc.std^2))"/>
<Constant symbol="Tc.ln_std" value="sqrt(ln(1+Tc.std^2/Tc.mean^2))"/>
<Constant symbol="v" name="neogenesis" value="3.3"/>
<Constant symbol="d" name="apoptosis" value="0.03"/>
<Constant symbol="time.onset" value="16.3"/>
<Constant symbol="time.duration" value="20"/>
<Constant symbol="k.act" value="0.03"/>
<Constant symbol="k.inact" value="1.0"/>
<Constant symbol="time.start" value="5.0"/>
<Constant symbol="time.apoptotic" value="1.0"/>
<Function symbol="N_WT">
<Expression>celltype.Cell_WT_p.size+celltype.Cell_WT_q.size</Expression>
</Function>
<Function symbol="N_p35">
<Expression>celltype.Cell_p35_p.size+celltype.Cell_p35_q.size</Expression>
</Function>
<Variable symbol="ode.Np_WT" value="3.0"/>
<Variable symbol="ode.Nq_WT" value="41.0"/>
<Variable symbol="ode.Np_p35" value="3.0"/>
<Variable symbol="ode.Nq_p35" value="41.0"/>
<Function symbol="ode.Nsum_WT">
<Expression>ode.Np_WT+ode.Nq_WT</Expression>
</Function>
<Function symbol="ode.Nsum_p35">
<Expression>ode.Np_p35+ode.Nq_p35</Expression>
</Function>
<System time-step="0.001" solver="Dormand-Prince [adaptive, O(5)]">
<DiffEqn symbol-ref="ode.Np_WT">
<Expression>(time>=5.0)*(v*ode.Np_WT/ode.Nsum_WT + k.act*ode.Nq_WT - k.inact*ode.Np_WT + ln(2)/Tc.mean*ode.Np_WT - d*(time>=time.onset)*(time<(time.onset+time.duration))*ode.Np_WT)</Expression>
</DiffEqn>
<DiffEqn symbol-ref="ode.Nq_WT">
<Expression>(time>=5.0)*(v*ode.Nq_WT/ode.Nsum_WT - k.act*ode.Nq_WT + k.inact*ode.Np_WT - d*(time>=time.onset)*(time<(time.onset+time.duration))*ode.Nq_WT)</Expression>
</DiffEqn>
<DiffEqn symbol-ref="ode.Np_p35">
<Expression>(time>=5.0)*(v*ode.Np_p35/ode.Nsum_p35 + k.act*ode.Nq_p35 - k.inact*ode.Np_p35 + ln(2)/Tc.mean*ode.Np_p35)</Expression>
</DiffEqn>
<DiffEqn symbol-ref="ode.Nq_p35">
<Expression>(time>=5.0)*(v*ode.Nq_p35/ode.Nsum_p35 - k.act*ode.Nq_p35 + k.inact*ode.Np_p35)</Expression>
</DiffEqn>
</System>
<Constant symbol="mcs_duration" value="0.01"/>
</Global>
</MorpheusModel>

Downloads
Files associated with this model: